UQ for Model-Form Uncertainties

We have proposed a stochastic formulation enabling the representation of model-form uncertainties in MD simulations, given a set of model candidates identified through domain expertise or learned using machine learning (ML). The approach relies on a reduced-order model, the projection basis of which is randomized on a subset of the Stiefel manifold characterized by a set of linear constraints defining, e.g., Dirichlet boundary conditions in the physical space.

Figures below show an application to an argon crystal melt; see the figure below.

Argon Before Melt — Argon before melting occurs

Argon After Melt — Argon after phase transformation

The approach allows for sampling over the matrix manifold, within the convex hull defined by the model candidates:

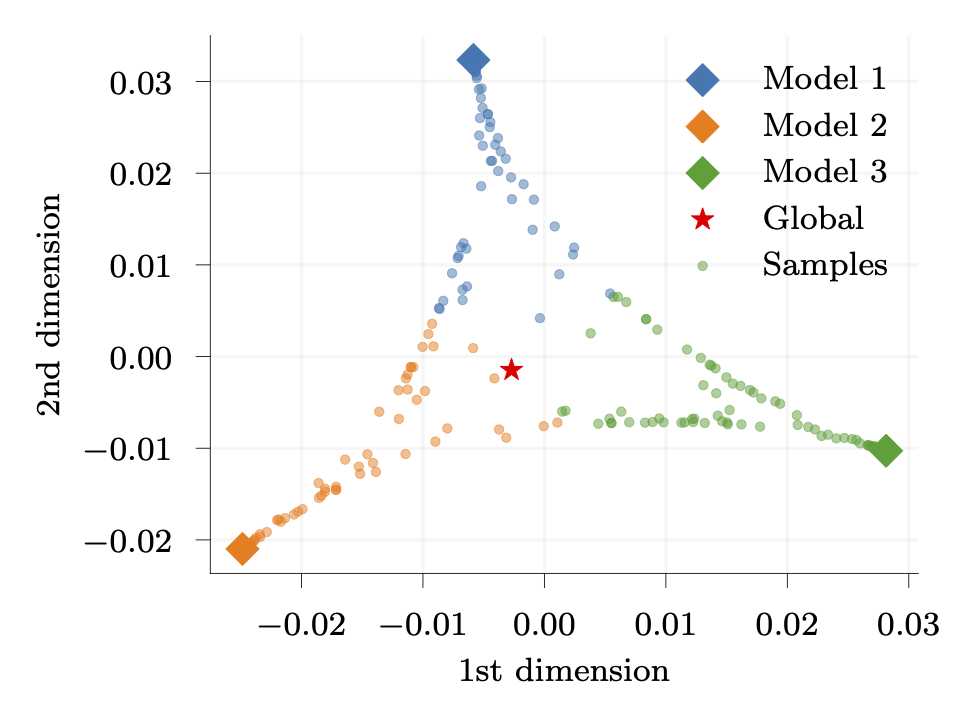
Sampling on the Stiefel Manifold — Samples of the ROB on a subset of the Stiefel manifold (visualization using spectral embedding)

Uncertainty propagation is then conducted to quantify the impact on macroscopic properties:

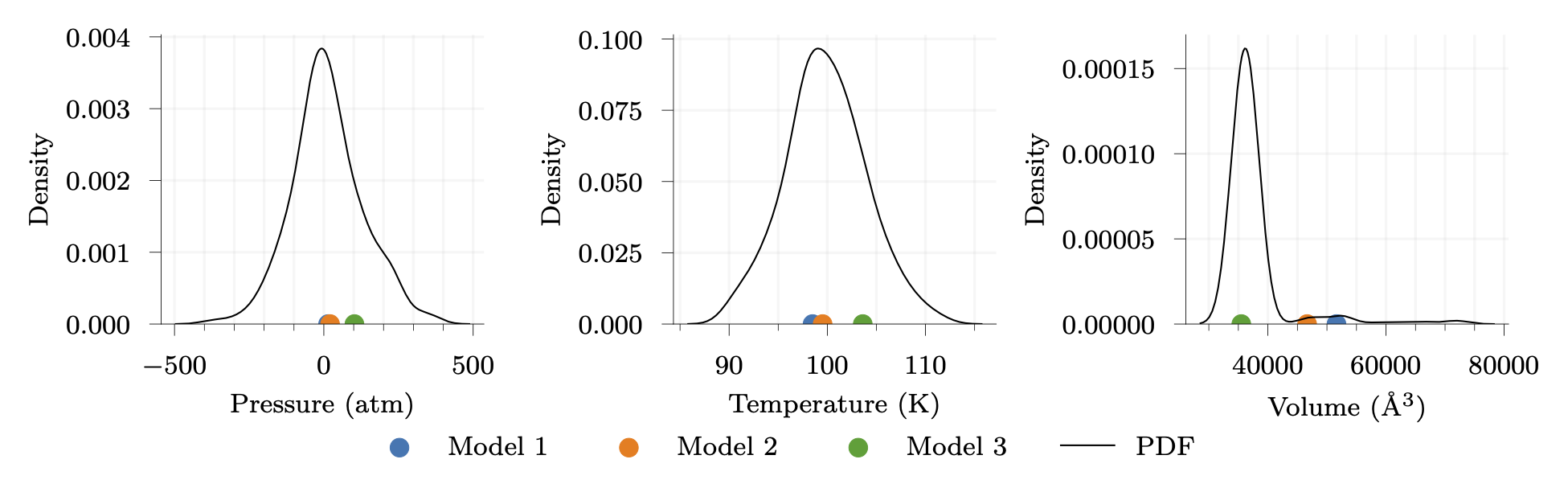
UQ Propagation Results — Uncertainty propagation results: PDFs of macroscopic properties, compared with the predictions from the model candidates.

Additional details can be found in the following papers:

H. Zhang and J. Guilleminot, A Riemannian stochastic representation for quantifying model uncertainties in molecular dynamics simulations, Computer Methods in Applied Mechanics and Engineering, 403, 115702 (2023)
S. Kounouho, R. Dingreville, and J. Guilleminot, Stochastic symplectic reduced-order modeling for model-form uncertainty quantification in molecular dynamics simulations in various statistical ensembles, Computer Methods in Applied Mechanics and Engineering, 431, 117323 (2024)