In this project (partly funded by the French National Research Agency within the frame of the MOSAIC project), we have investigated the construction, identification and validation of a stochastic representation modeling, in a tensorial form, the mechanical properties at the interphase between silica nanofillers and a surrounding polymer matrix.
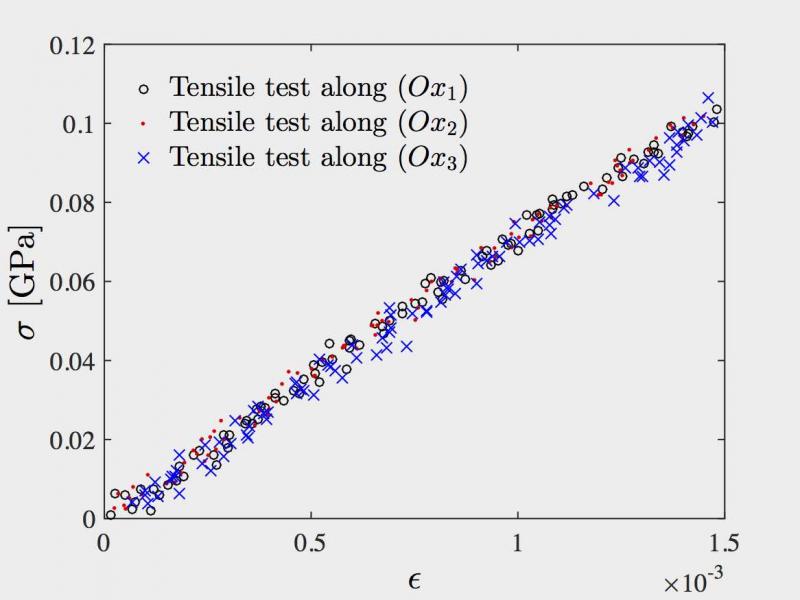
To this aim, MD simulations involving up to one million particles are used in order to resolve fine-scale physics and provide a numerical database on macroscopic properties. A snapshot of the MD box for a nanocomposite made up of an amorphous polymer (containing 80 long chains, each of which being composed of 1,000 CH2 sites) reinforced by a silica nanoinclusion (radius: 3 [nm]) is shown below (left panel), together with results from MD virtual testing (right panel).
Image

| Image
|
Running large-scale MD computations on the nanocomposite: snapshot of the system and virtual testing
These computations were subsequently plugged into a statistical inverse problem involving computational homogenization methods, with the aim to calibrate the hyperparameters defining the nongaussian random field model. A comparison of the multiscale predictions based on either the atomistic computations or the stochastic continuum model was finally discussed in a validation step. In particular, the realizations of the macroscopic stiffness tensor were compared with the envelopes of the probability density functions obtained by means of stochastic continuum simulations (see the figure below).
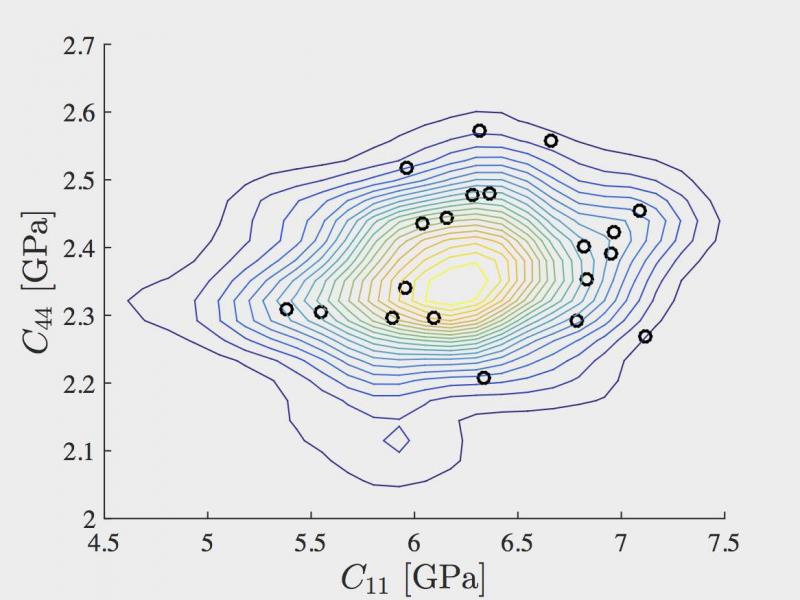
Comparing the joint PDF estimated from stochastic simulations (solid lines) with realizations from the MD computations (black circles)
For further details, please refer to the following publication:
- T. T. Le, J. Guilleminot and C. Soize, Stochastic continuum modeling of random interphases from atomistic simulations. Application to a polymer nanocomposite, Computer Methods in Applied Mechanics and Engineering, 303, 430-449 (2016)