This project, performed in collaboration with Prof. A. Asadpoure and Prof. M. Tootkaboni from the University of Massachusetts Dartmouth, aims at proposing a paradigm for topological optimization under uncertainties where stochastic fields are defined on the fly (at each design iteration) to account for process-introduced variability, rather than on the initial geometry. This introduces topological optimization under topologically-dependent uncertainties.
To develop the framework, a two-step approach was proposed. In the early stages of optimization, deterministic optimization is used to update the geometrical configuration to the point where the shape becomes manufacturable. This manufacturability condition is tracked by means of a statistical characterization on the density; see below.

Evolution of the PDF associated with the density, for several design iteration (SIMP method)
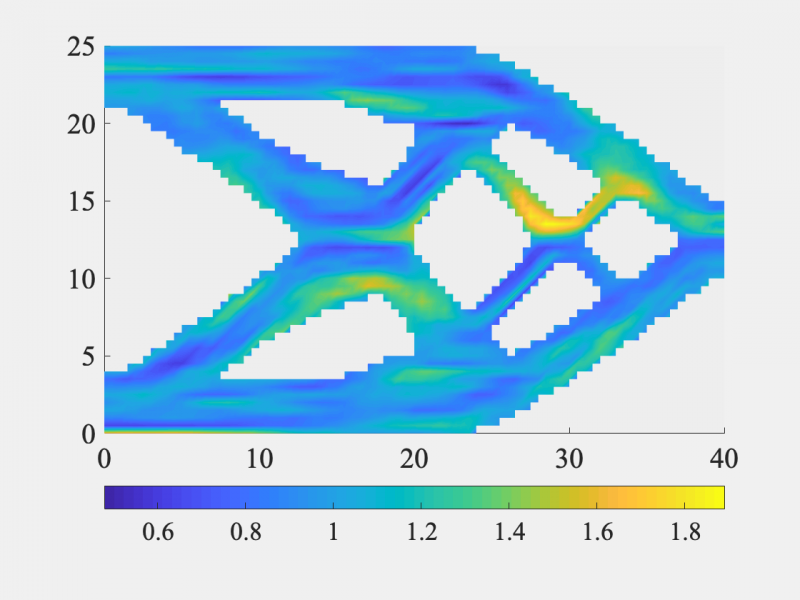
The stochastic method is subsequently deployed to define and simulate realizations of the random fields of material parameters automatically, at each iteration of the optimization solver. The rationale behind this updating is to account for (potentially) different processing conditions raised by the evolution of the geometry. The approach enables the introduction of various anisotropic features on the complex domain, as can seen in the figure below.
Image

| Image
|
Samples of an elastic field, for isotropic (left) and anisotropic (right) covariance kernels
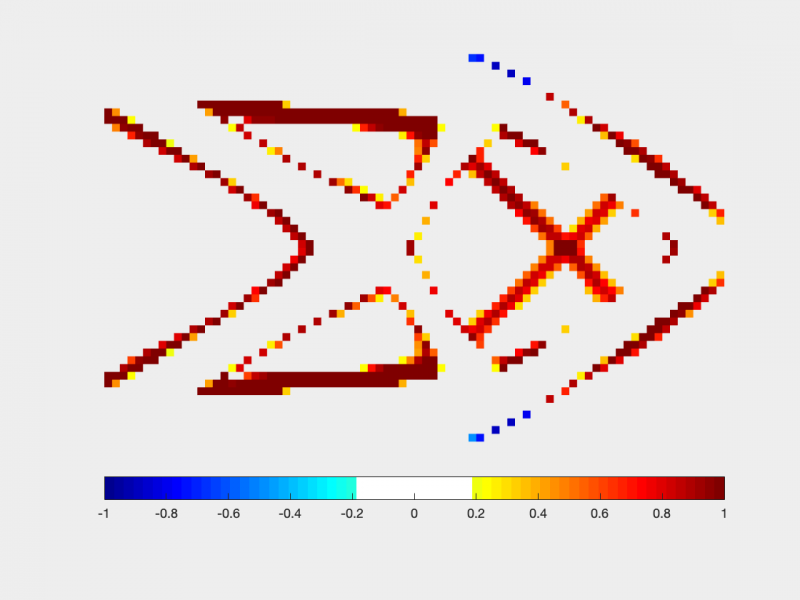
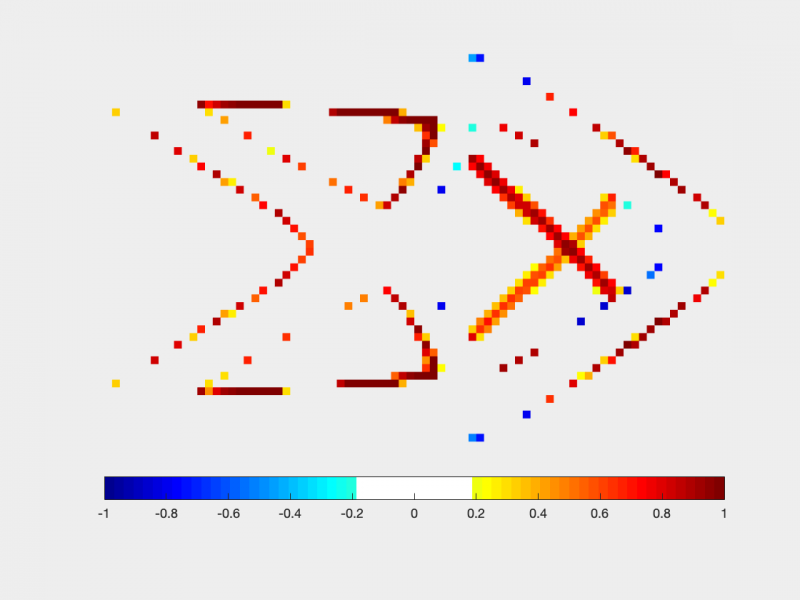
The impact of such topologically-dependent fields on the solution can be significant, and a comparison between a deterministic solution and the solutions obtained with the kernels introduced in the figure above is illustrated below.
Image
| Image
|
Difference between the deterministic solution and the solutions obtained with the isotropic (left) and anisotropic (right) kernels
This framework allows for a better integration of material processing at the optimization stage, and recovers most standard setups as specific cases.
For further details, please refer to the following publication:
- J. Guilleminot, A. Asadpoure and M. Tootkaboni, Topology optimization under topologically dependent material uncertainties, Structural and Multidisciplinary Optimization, 60, 1283-1287 (2019)