Brittle fracture in heterogeneous materials is a complex, multiscale phenomenon. While theoretical frameworks and computational methods enabling the simulation of crack propagation at micro- and macro-scales emerged over the past two decades, methodologies bridging information and variability across relevant scales are still to be developed.
In a first project, conducted in collaboration with Prof. Yvonnet (MSME, UPE) and Prof. Bornert (Navier, ENPC), we have advanced new methodologies that incorpore both multiscale features and stochastic aspects in the description of brittle fracture for random media (Ph.D. project of D.-A. Hun).
Image

| Image
|
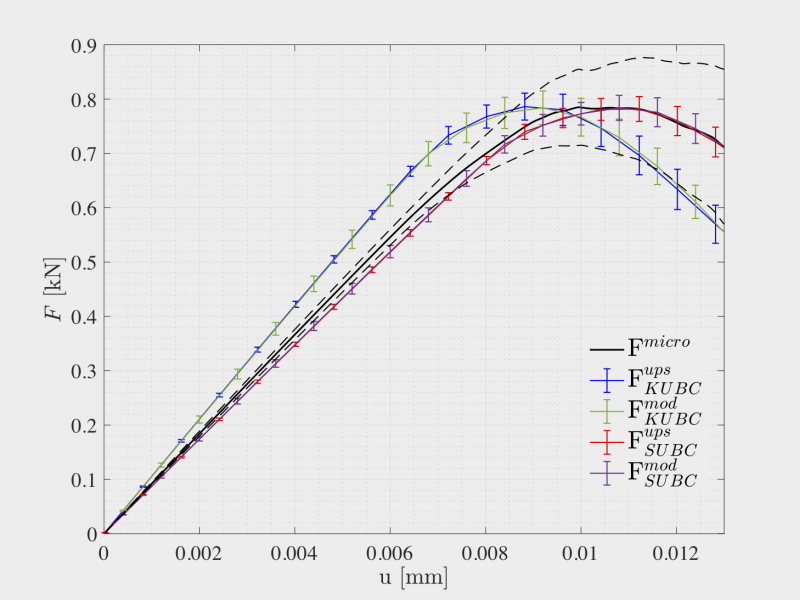
Left: Crack path predicted by the phase field formulation at microscale (monodisperse random microstructure). Right: Comparison of the macroscopic response between microscale and mesoscale formulations
For further details, please refer to the following publication:
- A. Hun, J. Guilleminot, J. Yvonnet and M. Bornert, Stochastic multi-scale modeling of crack propagation in random heterogeneous media, International Journal for Numerical Methods in Engineering, 119, 1325-1344 (2019)
In a second project, we have developed stochastic models for fracture properties, and discussed the identification of these models based on macroscopic, physical data (collaboration with T. Hu and Prof. Dolbow). We have, in particular, that the proposed formulation enables the reproduction of observed crack networks, both qualitatively (sample-wise) and in a statistical sense (see below).

Comparison between the probability density functions of fragment size, estimated from physical experiments (black) and from the calibrated model with stochastic fracture properties (red)
For further details, please refer to the following publication:
- T. Hu, J. Guilleminot, J. Dolbow, A Phase-Field Model of Fracture with Frictionless Contact and Random Fracture Properties: Application to Thin-Film Fracture and Soil Dessication, Computer Methods in Applied Mechanics and Engineering, 368, 113106 (2020)
In a third project funded in part by SANDIA, we also proposed a hybrid approach combining probabilistic learning and a proper Markovianization, which enables the sampling of additional crack paths based on a reference dataset (digitally synthesized here by using an appropriate phase-field formulation). The methodology allows one to circumvent data limitation, whether it be in computational or experimental settings, through statistical sampling.

Reference dataset (black), generated through the phase-field formulation, and newly generated crack patterns (red), obtained by combining probabilistic learning and a Markov description of crack paths
For further details, please refer to the following publication:
- J. Guilleminot and J. E. Dolbow, Data-Driven Enhancement of Fracture Paths in Random Composites, Mechanics Research Communications, 103, 103443 (2020)