By enabling the processing of parts with unprecedented levels of complexity over multiple length scales, additive manufacturing (AM) has opened new realms in terms of on-demand manufacturing for a wide class of engineered and biological materials. While transformative, AM technologies also raise formidable challenges with regard to material characterization, simulations for design and optimization, and certification and qualification. In particular, capturing the stochasticity introduced by processing conditions is a daunting challenge.
In a first project, supported by the National Science Foundation (under awards CMMI-1726403 and CMMI-1942928), we developed a methodology enabling the representation, sampling, and identification of spatially-dependent stochastic material parameters on complex structures produced by additive manufacturing.

Field of stochastic material parameter on a 3D-printed titatium scaffold
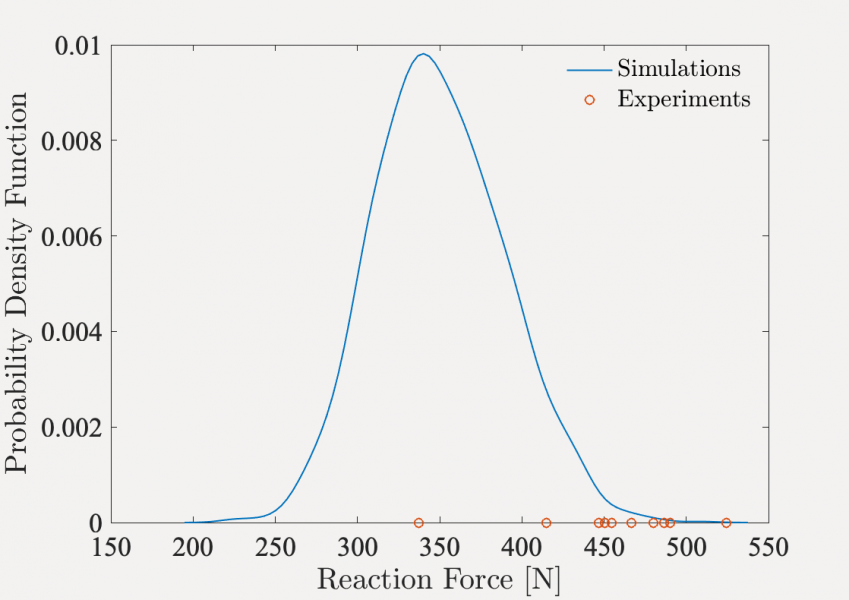
The modeling component relies on the combination of two ingredients. First, a fractional stochastic partial differential equation is introduced and parameterized in order to automatically capture the complex features of additively manufactured parts. Information-theoretic transport maps are subsequently introduced with the aim of ensuring well-posedness in the forward propagation problem. The identification of stochastic elasticity tensors on titanium scaffolds produced by laser powder bed fusion was subsequently discussed. To this end, we considered an isotropic approximation at a mesoscale where fluctuations are aggregated over several layers, and addressed both the calibration and validation of the probabilistic model by using different sets of physical structural experiments. Despite the high sensitivity of the forward map to applied boundary conditions, geometrical parameters, and structural porosity, it was shown that the calibrated stochastic model can generate non-vanishing probability levels for all experimental observations (see the figures below).
Image
 | Image
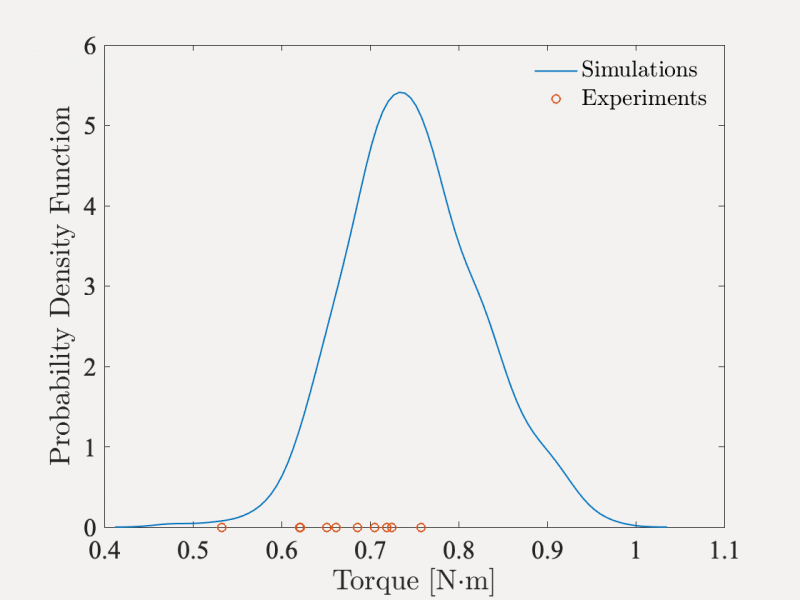 |
Results obtained for compression (left) and torsion (right) tests. Red circles represent experimental samples, while the blue lines are the probability density functions estimated with the model
In a second project, we addressed the modeling of the geometrical perturbations induced by the AM technology. These perturbations play a critical role for highly porous structures as they dramatically affect load bearing capacity and ultimate failure of the component.

Realization of the field of geometrical perturbation on a 3D-printed gyroid structure
For further details, please refer to the following publications:
- S. Chu, J. Guilleminot, C. Kelly, B. Abar and K. Gall, Stochastic modeling and identification of material parameters on structures produced by additive manufacturing, Computer Methods in Applied Mechanics and Engineering, 387, 114166 (2021)
- H. Zhang, J. Guilleminot and L. Gomez, Stochastic modeling of geometrical uncertainties on complex domains, with application to additive manufacturing and brain interface geometries, Computer Methods in Applied Mechanics and Engineering, 385, 114014 (2021)