Taking into account uncertainties in computational models requires the construction of suitable probabilistic models. On the one hand, these models must ensure some fundamental properties for the operators involved in the associated stochastic boundary value problem (SBVP): such properties allow one to prove, in particular, the existence and uniqueness of the solution to the SBVP. On the other hand, the stochastic representations must faithfully reproduce the underlying physical phenomena, without introducing an arbitrary modeling bias.
In this context, we have proposed, identified and validated new classes of tensor-valued random fields. Additionally, new generators relying on families of stochastic differential equations were constructed in order to sample fields with values on highly-constrained matrix sets. Such models are useful for the modeling of stochastic elliptic operators, such as those entering formulations in linear elasticity or in the simulation of Darcean flows.
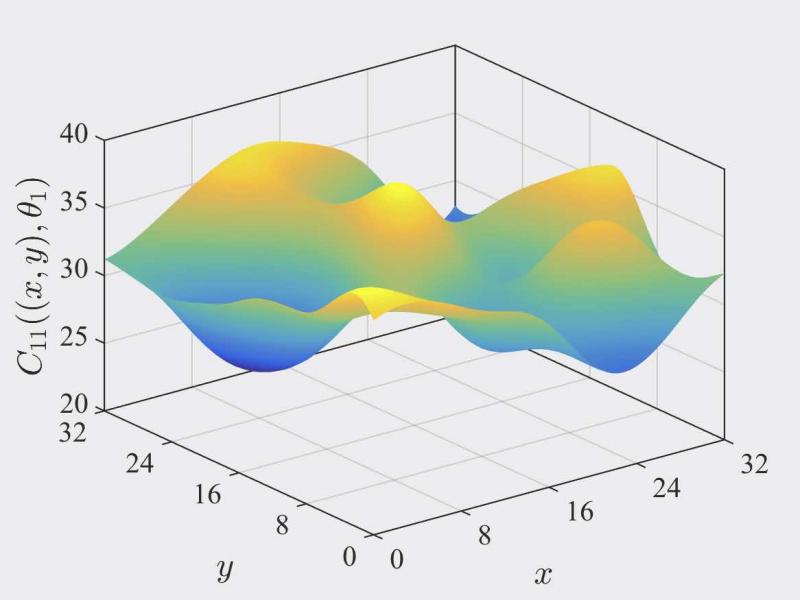
Various applications were proposed, including the modeling of elasticity and permeability random fields, or the modeling of random interphases in nanocomposites. An illustration for elasticity random fields that are orthotropic almost surely can be found in the figure below.
Image
 | Image
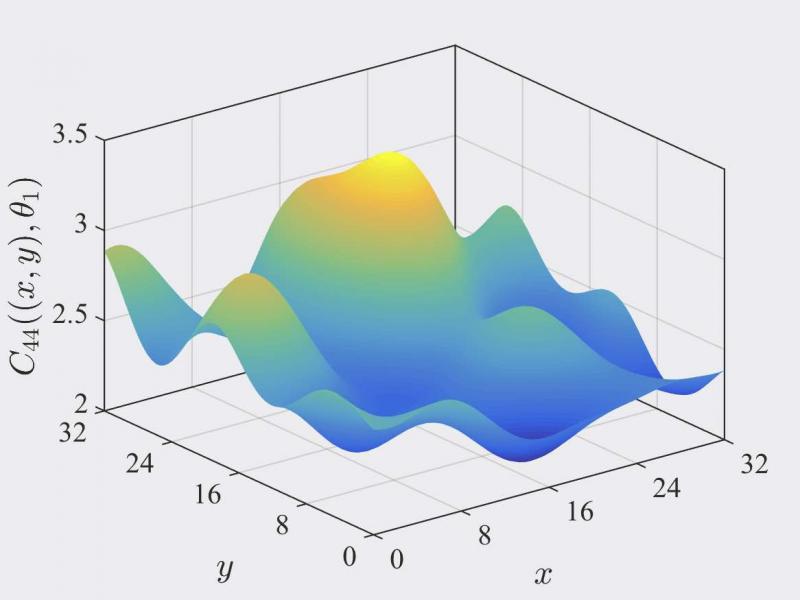 |
Realizations of the random fields modeling the components (11) and (44) of the elasticity tensor
For further details, please refer to the following (selected) publications:
- S. Chu and J. Guilleminot, Stochastic multiscale analysis with random fields of material properties defined on non-convex domains, Mechanics Research Communications, 97, 39-45 (2019)
- B. Staber and J. Guilleminot, Stochastic modeling and generation of random fields of elasticity tensors: a unified information-theoretic approach, Comptes-Rendus Mécanique (Proceedings of the French Academy of Sciences), 345, 399-416 (2017)
- B. Staber and J. Guilleminot, Approximate solutions of Lagrange multipliers for information-theoretic random field models, SIAM/ASA Journal on Uncertainty Quantification, 3, 559-621 (2015)
- J. Guilleminot and C. Soize, Itô SDE-based generator for a class of non-Gaussian vector-valued random fields in uncertainty quantification, SIAM Journal of Scientific Computing, 36(6), A2763-A2786 (2014)
- J. Guilleminot and C. Soize, Random fields with symmetry properties: Application to the mesoscopic modeling of elastic random media, SIAM Multiscale Modeling & Simulation, 11(3), 840-870 (2013)
- J. Guilleminot and C. Soize, On the statistical dependence for the components of random elasticity tensors exhibiting material symmetry properties, Journal of Elasticity, 111(2), 109-130 (2013)
- J. Guilleminot, C. Soize and R. Ghanem, Stochastic representation for anisotropic permeability tensor random fields, International Journal for Numerical and Analytical Methods in Geomechanics, 36(13), 1592-1608 (2012)
- J. Guilleminot, A. Noshadravan, R. Ghanem and C. Soize, A probabilistic model for bounded elasticity tensor random fields with application to polycrystalline microstructures, Computer Methods in Applied Mechanics and Engineering, 200(17-20), 1637-1648 (2011)
- J. Guilleminot and C. Soize, Non-Gaussian positive-definite matrix-valued random fields with constrained eigenvalues: application to random elasticity tensors with uncertain material symmetries, International Journal for Numerical Methods in Engineering, 88(11), 1128-1151 (2011)